Scope and theoretical considerations
Perhaps the most significant "formal" achievement of the modern evolutionary synthesis has been the framework of mathematical population genetics. Indeed some authors (Beatty 1986) would argue that it does define the core of the modern synthesis.
Lewontin (1974) outlined the theoretical task for population genetics. He imagined two spaces: a "genotypic space" and a "phenotypic space". The challenge of a complete theory of population genetics is to provide a set of laws that predictably map a population of genotypes (G1) to a phenotype space (P1), where selection takes place, and another set of laws that map the resulting population (P2) back to genotype space (G2) where Mendelian genetics can predict the next generation of genotypes, thus completing the cycle. Even leaving aside for the moment the non-Mendelian aspects revealed by molecular genetics, this is clearly a gargantuan task. Visualizing this transformation schematically:
(adapted from Lewontin 1974, p. 12). XD
T1 represents the genetic and epigenetic laws, the aspects of functional biology, or development, that transform a genotype into phenotype. We will refer to this as the "genotype-phenotype map". T2 is the transformation due to natural selection, T3 are epigenetic relations that predict genotypes based on the selected phenotypes and finally T4 the rules of Mendelian genetics.
In practice, there are two bodies of evolutionary theory that exist in parallel, traditional population genetics operating in the genotype space and the biometric theory used in plant and animal breeding, operating in phenotype space. The missing part is the mapping between the genotype and phenotype space. This leads to a "sleight of hand" (as Lewontin terms it) whereby variables in the equations of one domain, are considered parameters or constants, where, in a full-treatment they would be transformed themselves by the evolutionary process and are in reality functions of the state variables in the other domain. The "sleight of hand" is assuming that we know this mapping. Proceeding as if we do understand it is enough to analyze many cases of interest. For example, if the phenotype is almost one-to-one with genotype (sickle-cell disease) or the time-scale is sufficiently short, the "constants" can be treated as such; however, there are many situations where it is inaccurate.
Population geneticists
The three founders of population genetics were the Britons R.A. Fisher and J.B.S. Haldane and the American Sewall Wright. Fisher and Wright had some fundamental disagreements and a controversy about the relative roles of selection and drift continued for much of the century between the Americans and the British. The Frenchman Gustave Malécot was also important early in the development of the discipline. John Maynard Smith was Haldane's pupil, whilst W.D. Hamilton was heavily influenced by the writings of Fisher. The American George R. Price worked with both Hamilton and Maynard Smith. On the American side, Richard Lewontin and the Japanese Motoo Kimura were heavily influenced by Wright.

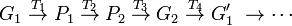










No comments:
Post a Comment